06. 관계 데이터 연산

관계 데이터 연산을 일반 집합 연산자와 순수 관계 연산자로 나누어 학습한다.

6.1. 관계 데이터 연산의 개념

관계 데이터 모델에서 원하는 데이터를 추출하기 위해 릴레이션에 처리를 요구하는 것으로, 관계 대수와 관계 해석으로 나눌 수 있다.

관계 대수(relational algebra)는 데이터의 처리 과정을 순서대로 기술하는 절차 언어이고,
관계 해석(relational calculus)는 원하는 데이터가 무엇인지만 기술하는 비절차적 언어이다.

이 둘은 개념적 언어로 실제 사용되지는 않는다. 하지만 데이터 언어의 유용성을 검증하는 도구로써 쓰인다.

관계 대수는 원하는 결과를 얻기 위해 릴레이션을 처리하는 과정을 순서대로 기술하는 절차적 언어이다.

관계대수는 연산자들의 집합으로 정의될 수 있고, 피연산자와 연산의 결과값은 모두 릴레이션이다.

다음 중 합집합, 교집합, 차집합의 경우 피연산자인 2개의 릴레이션이 합병 가능(union-compatible)해야 한다.

합집합
- R ∪ S
- R ∪ S = S ∪ R
- (R ∪ S) ∪ T = R ∪ (S ∪ T)
- 중복 데이터는 배제한다.
교집합
- R ∩ S
- R ∩ S = S ∩ R
- (R ∩ S) ∩ T = R ∩ (S ∩ T)
- 중복 데이터는 배제한다.
차집합
- R - S
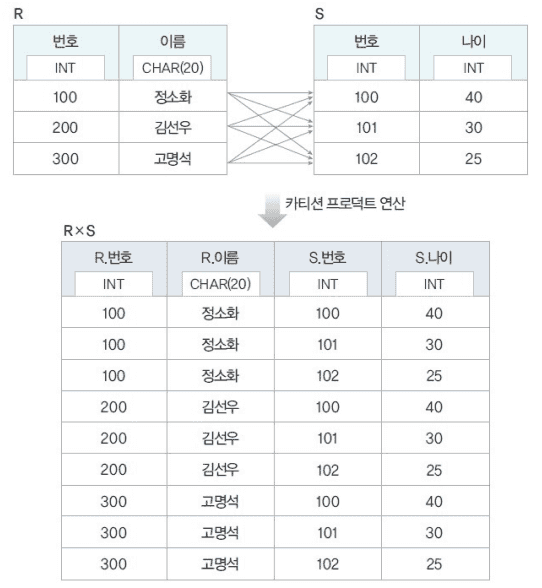
카티션 프로덕트(Cartesian Product)
- R X S
- R X S = S X R
- (R X S) X T = R X (S X T)
- 동일한 이름의 속성의 경우 릴레이션 이름을 앞에 붙인다(Ex. R.번호)
- 차수 = R의 차수 + S의 차수
- 카디널리티 = R의 카디널리티 * S의 카디널리티

셀렉트
조건식을 만족하는 투플(행)을 선택하여 새로운 릴레이션으로 반환
- σ조건식(릴레이션)
- σheight>170(Person)
- σ조건식1(σ조건식2(릴레이션)) = σ조건식2(σ조건식1(릴레이션)) = σ조건식1 ^ 조건식2(릴레이션)
프로젝트
조건식을 만족하는 속성(열)을 선택하여 새로운 릴레이션으로 반환
- π속성리스트
- πname, height(Person)
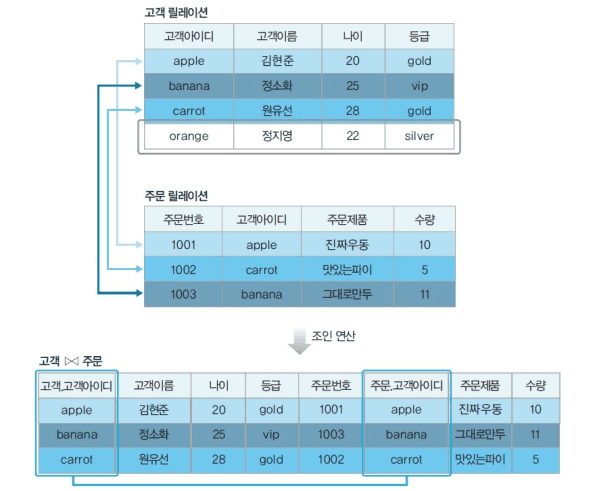
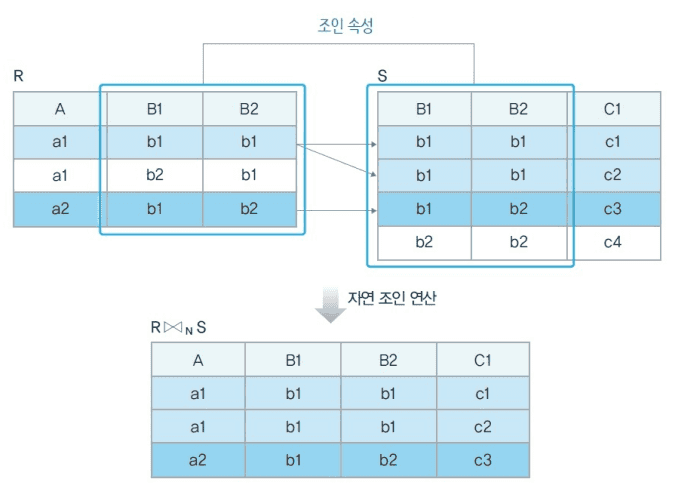
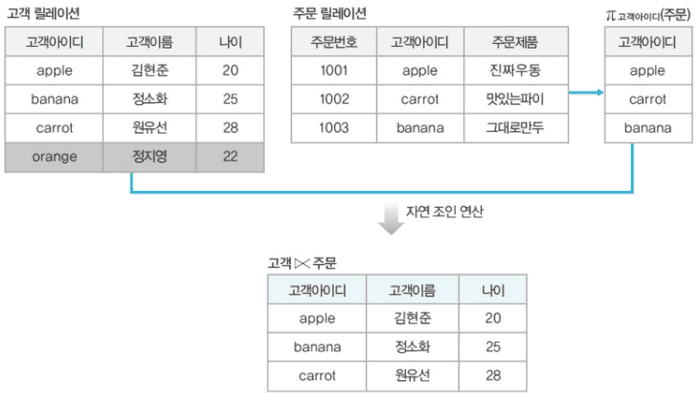
조인
두 릴레이션에서 조인 속성 값이 조건식을 만족하는 투플에 대해 새로운 릴레이션을 만들어 반환. 동일한 속성 이름의 경우 '릴레이션이름.속성이름' 형식으로 표기한다.
- 세타 조인 조건식을 만족하는 투플끼리만 연결하여 새로운 릴레이션을 만들어 반환
  - R ⋈AθB S
  - A는 릴레이션 R의 속성, B는 릴레이션 S의 속성
  - θ에는 비교연산자(>, >=, <, <=, =, !=)가 들어간다.
- 동등 조인
  세타 조인 중 θ가 = 인 조인
  - R ⋈A=B S
- 자연 조인
  두 릴레이션의 중복된 속성이 모두 일치하는 투플만을 합친 릴레이션
  - R ⋈N S
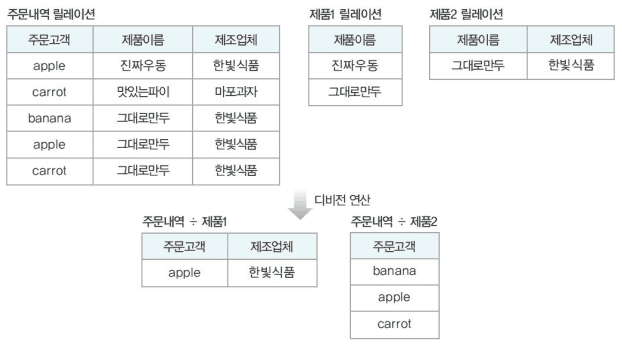
디비전
R의 속성이 S이 속성값을 모두 가진 투플에서 S가 가진 속성을 제외한 속성만을 구해서 새로운 릴레이션으로 반환.
- R ÷ S

등급이 gold인 고객의 이름과 나이를 검색하시오.
π이름, 나이(σ등급=gold(고객))
고객이름이 원유선인 고객의 등급과, 원유선 고객이 주문한 주문제품, 수량을 검색하시오.
π등급, 주문제품, 수량(σ고객이름=원유선(고객))
주문수량이 10개 미만인 주문 내역을 제외하고 검색하시오.
σ수량>10(주문)

세미 조인
두 릴레이션이 모든 속성을 표현하지 않고, 연산자 앞의 릴레이션의 속성만을 표기하는 조인방법
- R ⋉ S
- R ⋉ S != S ⋉ R
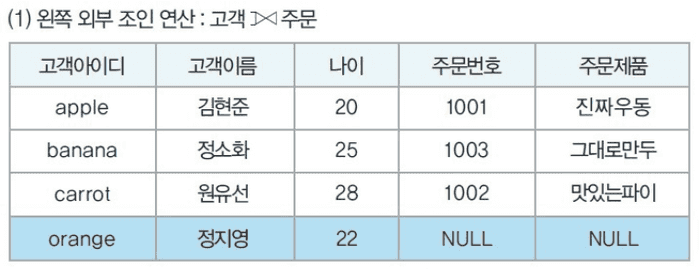
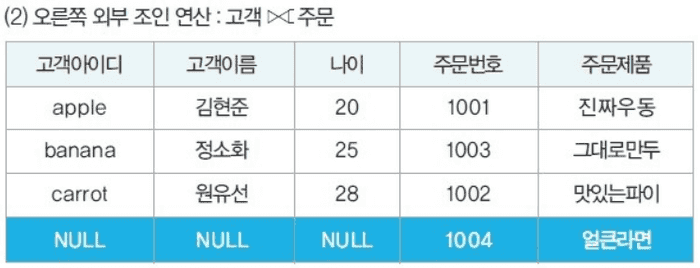
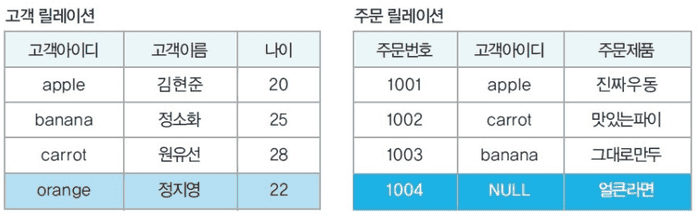
외부 조인
두 릴레이션에서 공통 속성이 있는 튜플 뿐만 아니라, 그렇지 않은 튜플들도 가져와 빈 데이터를 null로 채워 표시한다.
- R ⟕ S (왼쪽 외부 조인)
- R ⟖ S (오른쪽 외부 조인)
- R ⟗ S (완전 외부 조인)