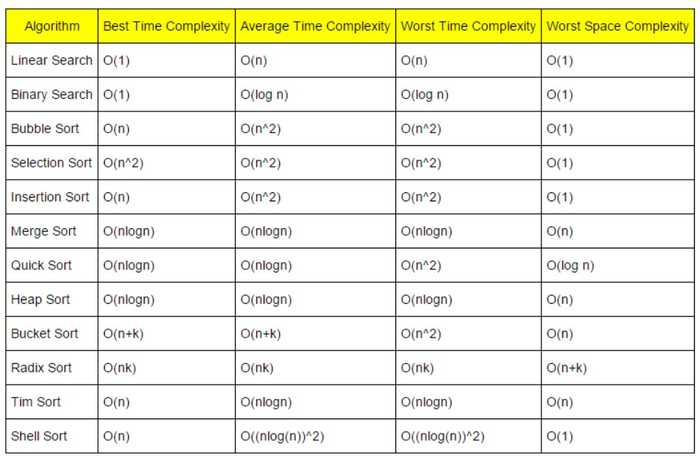
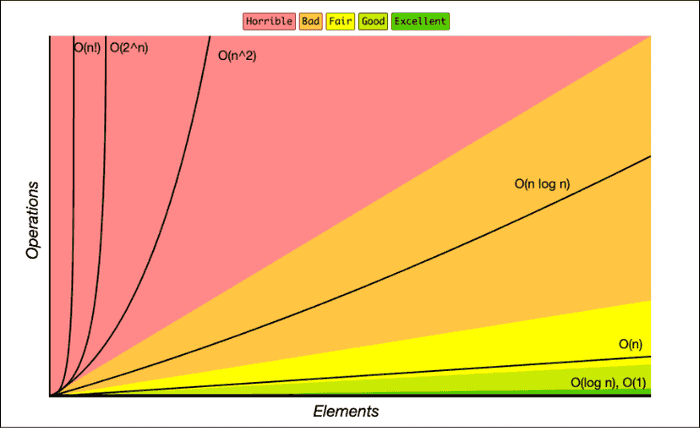
정렬(Sorting) 알고리즘 정리
면접에서 탈탈 털린 후 작성한 정렬 관련 알고리즘을 총정리
- 1. Bubble Sort (거품 정렬)
- 2. Selection Sort (선택 정렬)
- 3. Insertion Sort (삽입 정렬)
- 4. Shell Sort (셸 정렬)
- 5. Heap Sort (힙 정렬)
- 6. Merge Sort (병합 정렬)
- 7. Quick Sort (퀵 정렬)
- 8. Counting Sort (계수 정렬)
- 9. 복잡도 비교
1. Bubble Sort (거품 정렬)
가장 시간복잡도가 높은 알고리즘이기 때문에 사용을 추천하지 않는다.
단 정렬이 완료되었는지를 루프마다 판단할 수 있어서, 거의 정렬이 된 데이터에 대해서는 유효한 성능을 낼 수 있다.
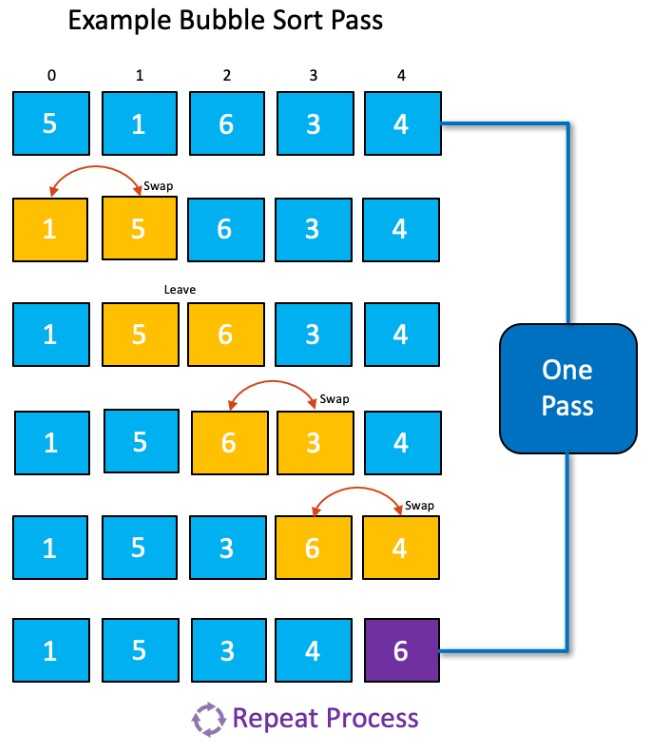
1.1. 동작 과정
- 0 ~ n-1 번 인덱스에 대해서 현재 숫자와 뒤의 숫자를 비교한다. 현재 숫자가 더 클 경우 스왑한다.
그 결과 뒤에서 첫번째 수는 배열에서 첫번째로 큰 수가 자리한다. - 0 ~ n-2 번 인덱스에 대해서 현재 숫자와 뒤의 숫자를 비교한다. 현재 숫자가 더 클 경우 스왑한다.
그 결과 뒤에서 두번째 수는 배열에서 두번째로 큰 수가 자리한다.
... - 0 ~ 0 번 인덱스에 대해서 대해서 현재 숫자와 뒤의 숫자를 비교한다. 현재 숫자가 더 클 경우 스왑한다.
그 결과 뒤에서 N-1 번째 수는 배열에서 N-1번째로 큰 수가 자리한다.
1.2. 복잡도
- 공간복잡도 O(1)
주어진 배열 내에서 스왑하며 연산이 이뤄지기 때문에 추가 메모리를 필요로 하지 않는다. - 시간복잡도 O(n**2)
비교와 스왑 연산이 (n-1 + n-2 + n-3 + .... + 3 + 2 + 1)회 일어난다.

(단, 최선의 경우 O(n)의 복잡도를 가진다.)
1.3. Python 구현
def bubble_sort(nums):
N = len(nums)
# 배열의 길이에 대응하는 횟수만큼 루프를 돈다.
for i in range(N):
is_swapped = False # 루프에 대해서 스왑여부를 판단하는 플래그
# 스왑여부를 탐색하는 배열 길이를 하나씩 줄여나간다.
# 루프를 돌 때마다, 탐색한 배열에서 가장 큰 숫자가 순서대로 뒷쪽에 쌓이기 때문.
for j in range(N - i -1):
if nums[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j] # 현재 숫자가 뒤의 숫자보다 클 경우, 스왑
is_swapped = True # 플래그를 바꿔준다
if not is_swapped: # 루프에 대해서 한 번도 스왑이 일어나지 않았으면, 정렬 완료
return nums
return nums
2. Selection Sort (선택 정렬)
2.1. 동작 과정
- 0 ~ n-1번 인덱스 중 가장 작은 값을 찾아 0번 인덱스와 스왑한다.
- 1 ~ n-1번 인덱스 중 가장 작은 값을 찾아 1번 인덱스와 스왑한다.
... - n-2 ~ n-1번 인덱스 중 가장 작은 값을 찾아 n-2번 인덱스와 스왑한다.

2.2. 복잡도
- 공간복잡도 O(1)
주어진 배열 내에서 스왑하며 연산이 이뤄지기 때문에 추가 메모리를 필요로 하지 않는다. - 시간복잡도 O(n**2)
비교 연산이 (n-1 + n-2 + n-3 + .... + 3 + 2 + 1)회 일어나고, n-1번의 스왑 연산이 일어난다.

2.3. Python 구현
def selection_sort(nums):
N = len(nums)
# N-1 번 최솟값을 찾아낸다.
for i in range(N - 1):
min_idx = i # i번째 숫자를 포함(기준으로 삼음)
# i+1번째부터 순회하며 i번째 가장 작은 값을 탐색
for j in range(i + 1, N):
if nums[j] < nums[min_idx]:
min_idx = j
nums[i], nums[min_idx] = nums[min_idx], nums[i] # i번째 숫자와 i번째 작은 숫자를 스왑
return nums
3. Insertion Sort (삽입 정렬)
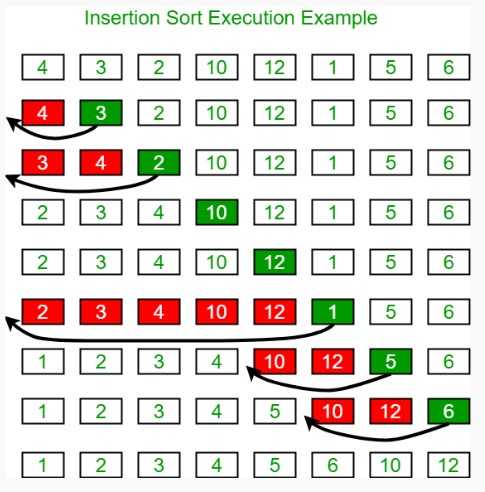
간단하게 말해 배열의 앞부분을 정렬된 배열, 뒷 부분을 정렬되지 않은 배열로 구분한다. 그리고 정렬되지 않은 배열의 가장 앞에 수를 꺼내서 정렬된 배열의 적절한 위치로 삽입한다.
3.1. 동작 과정
- 0 ~ 1번 인덱스 중 1번 인덱스 값이 들어갈 위치를 찾아 넣는다.
- 0 ~ 2번 인덱스 중 2번 인덱스 값이 들어갈 위치를 찾아 넣는다.
... - 0 ~ n-1번 인덱스 중 n-1번 인덱스 값이 들어갈 위치를 찾아 넣는다.
3.2. 복잡도
- 공간복잡도 O(1)
주어진 배열 내에서 스왑하며 연산이 이뤄지기 때문에 추가 메모리를 필요로 하지 않는다. - 시간복잡도 O(n**2)
비교 연산이 최대 (1 + 2 + 3 + .... + n-3 + n-2 + n-1)회 일어나고, n-1번의 스왑 연산이 일어난다.

(단, 정렬되어 있는 값의 경우 비교 연산만 n-1번 이루어져 O(n)의 시간복잡도를 가진다.)
3.3. Python 구현
def insertion_sort(nums):
N = len(nums)
# 1 ~ n-1 번 인덱스에 대해서 반복
for i in range(1, N):
cur_num = nums[i]
j = i - 1
# 왼쪽 배열에서 i번째 숫자가 들어갈 위치를 찾는다.
while j >= 0 and cur_num < array[j]:
array[j + 1] = array[j] # 숫자를 하나씩 오른쪽으로 민다.
j = j - 1
array[j + 1] = cur_num # i번째 숫자를 삽입
return nums
4. Shell Sort (셸 정렬)
삽입정렬을 보완하기 위한 알고리즘이다. 앞서 살펴본 것 처럼 쉘 알고리즘은 정렬이 잘 되어 있을수록 시간복잡도가 줄어든다. 비교연산을 해야할 횟수(거리)가 줄어들기 때문이다. 반대로 생각하면, 정렬을 위해 비교해야할 거리가 클 수록 시간 복잡도가 늘어난다.
위와 같은 특징에서 착안해서, 쉘 정렬은 배열의 전체적인 정렬도를 점차 높이는 방법으로 삽입 정렬을 수행한다. gap만큼 떨어진 숫자들을 하나의 부분 배열로 간주해서 삽입 정렬을 수행하고, 이 gap을 점차 1까지 줄여나간다.
4.1. 동작 과정
- gap의 초기 크기를 n // 2로 결정한다.
- gap ~ n-1번째 인덱스를 기준점으로 왼쪽 숫자들에 대해서 gap의 간격으로 부분배열을 만들고, 삽입정렬을 수행한다.
- gap의 크기를 2로 나눈다.
- gap의 크기가 1이 될 때까지 2 ~ 3의 과정을 반복한다.
4.2. 복잡도
- 공간복잡도 O(1)
주어진 배열 내에서 스왑하며 연산이 이뤄지기 때문에 추가 메모리를 필요로 하지 않는다. - 시간복잡도 O(n**2)
쉘 정렬과 동일하게 O(n**2)의 복잡도를 가진다.
그러나 최선과 평균 시간 복잡도가 O(n*log n)이다.
4.3. Python 구현
def shell_sort(nums):
N = len(nums)
gap = N // 2 # 첫 gap은 배열 크기의 반으로 지정한다.
while gap > 0: # gap이 1이 될 때까지 줄여나간다.
# gap의 크기만큼 간격을 띄고 shell 정렬을 수행한다.
for i in range(gap, N):
cur_num = nums[i]
j = i - gap
cur_num < array[j]:
while j >= gap and cur_num < nums[j]:
array[j] = array[j - gap]
j -= gap
array[j] = cur_num
gap //= 2 # gap은 2로 나눈 몫으로 줄여나간다
5. Heap Sort (힙 정렬)
자료구조 힙을 이용한 정렬 방법이다.
길이가 n인 heap 배열은 depth가 log n 이다.
- pop 연산 시, logN 번의 비교 및 치환이 일어난다.(Heapify)
- 정렬을 위해서 N번의 pop 연산이 일어난다.
따라서 힙을 이용한 연산의 시간 복잡도는 O(n * log n)dlek.
6. Merge Sort (병합 정렬)
분할 정복법 중 하나의 큰 문제를 여러 개의 작은 문제로 쪼개서, 작은 문제를 해결한 결과를 모아서 큰 문제의 답을 얻는다. 분할 정복 특징 상, 재귀로 구현된다.
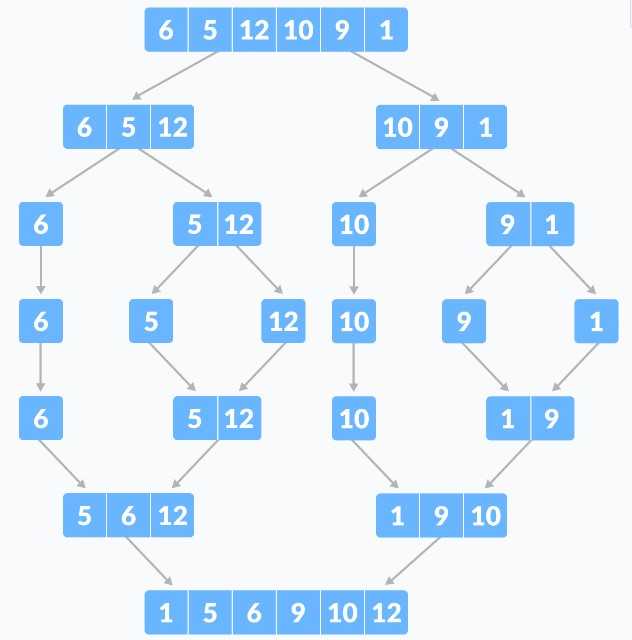
6.1. 동작 과정
- 배열의 길이가 1이 될 때 까지, 반으로 쪼갠다.(분할)
- 쪼개진 배열을 2개씩 비교 정렬하며 합친다.(병합)
6.2. 복잡도
- 공간복잡도 O(n)
배열을 병합할 때, 병합 결과를 담을 배열이 필요하므로 공간 복잡도 는 O(n)이다. - 시간복잡도 O(n*log n)
크기가 n인 데이터를 절반 씩 분할 했을 경우, 병합하는 깊이는 log n이다. 각 depth에 대해 병합 시에는 모든 데이터에 대해서 한 번씩 비교연산이 일어난다. O(n * log n)
6.3. Python 구현
def merge_sort(nums):
# 베이스 반환 조건: 1개 이하의 배열이 되면 반환한다.
if len(nums) < 2:
return nums
# 배열을 반으로 나눠서, 왼쪽과 오른쪽 배열에 대해 각각 재귀호출 한다.
mid = len(nums) // 2
left_arr = merge_sort(nums[:mid]) # left_arr는 왼쪽 배열이 정렬된 값이다.
right_arr = merge_sort(nums[mid:]) # right_arr는 오른쪽 배열이 정렬된 값이다.
# left_arr와 right_arr는 각 정렬된 값이다.
# left_arr와 right_arr를 앞에서부터 서로 비교하며 merged_arr에 작은 값을 merged_arr에 채워 넣는다.
l = r = 0
merged_arr = []
while l < len(left_arr) and r < len(right_arr): # 양 배열 중 적어도 하나를 탐색 완료할 때까지
if left_arr[l] < right_arr[h]:
merged_arr.append(left_arr[l])
l += 1
else:
merged_arr.append(right_arr[r])
r += 1
merged_arr += left_arr[l:]
merged_arr += right_arr[r:]
return merged_arr # left_arr와 right_arr를 병합해서 정렬한 값 반환
7. Quick Sort (퀵 정렬)
병합 정렬과 비슷하게 문제를 분할하면서 이뤄진다. 단 다음과 같은 차이점이 있다.
- 배열의 중간에 위치한 값 아닌 pivot값을 기준으로 분할한다. pivot 값을 기준으로 큰 숫자와 작은 숫자의 갯수가 동일할 수록 알고리즘이 효율적이다.
- 배열을 분할 할 때, 비교연산이 일어난다.
1번 기준에 따라 pivot값을 어떻게 선택하느냐에 따라서 시간 복잡도가 달라진다. 최대 O(n**2)까지 커질 수 있는 불안정한 정렬 알고리즘이다.
7.1. 동작 과정
- 배열의 pivot을 설정한다.
- pivot과 나머지 숫자를 비교 연산하여, pivot보다 작은 숫자 배열과, 큰 숫자 배열을 얻는다.
- 작은 숫자 배열과, 큰 숫자 배열에 대해서 (1 ~ 2)의 과정을 반복한다.
- 배열의 길이가 1이하로 쪼개지면 그대로 다시 합친다.
7.2. 복잡도
-
공간 복잡도
인메모리 정렬 방식을 사용할 경우, O(log n)의 공간복잡도로 구현 가능하다.뭔소린지 모르겠다 -
시간 복잡도
pivot값이 이상적으로 선택되었을 경우, 병합정렬과 마찬가지로 (log n)의 깊이의 대해서, 각각 n번의 비교 연산이 일어나므로 O(n*log n)의 복잡도를 가진다.그러나 최악의 경우 분할정복이 (n)의 깊이를 가지므로 O(n**2)의 복잡도를 가진다.
7.3. Python 구현
# 이 코드에서는 pivot을 병합 정렬과 동일하게 배열의 중간위치 값으로 설정한다.
def quick_sort(nums):
# 베이스 반환 조건: 1개 이하의 배열이 되면 반환한다.
if len(nums) <= 2:
return nums
pivot = nums[len(nums) // 2] # pivot 설정
lesser_arr, equal_arr, greater_arr = [], [], [] # 각각 pivot보다) 작은 숫자 배열, 동일한 숫자 배열, 큰 숫자 배열
for num in arr:
if num < pivot:
lesser_arr.append(num)
elif num > pivot:
greater_arr.append(num)
else:
equal_arr.append(num)
# pivot보다 작은 숫자배열과, pivot보다 큰 숫자 배열을 quick_sort에 재귀호출 한다.
# 결과를 그대로 이어 붙여 반환한다.
return quick_sort(lesser_arr) + equal_arr + quick_sort(greater_arr)
8. Counting Sort (계수 정렬)
특정한 조건이 만족할 때, O(n + k)의 시간복잡도로 정렬할 수 있다. 이 때 k는 배열에 존재하는 숫자의 크기 범위이다. 즉 k가 데이터의 갯수 n보다 작으면, **O(n)**의 정렬이 가능하다.
- 배열에 존재하는 모든 숫자가 0이상의 정수여야 한다.
- 배열에 존재하는 숫자의 크기 범위(k)가 지나치게 커서는 안된다.
8.1. 동작 과정
- 배열의 숫자 범위(k)에 해당하는
[0] * k의 누적합 예비 배열을 만든다. - 배열을 1회 순회하며, 숫자를 인덱스로 하는 누적합 예비 배열의 값을 +1 한다.
- 누적합 예비 배열을 누적합하여 누적합 배열을 만든다.
- 누적합 배열을 1회 순회하며, 값만큼 인덱스를 출력한다.
8.2. 복잡도
- 공간 복잡도 O(k)
숫자 범위(k)에 해당하는 배열을 생성해야 한다. - 시간 복잡도 O(n+k)
배열을 1회 순회 O(n)하고, 누적합 배열을 1회 순회 O(k)한다.
8.3. Python 구현
def counting_sort(nums, K):
N = len(nums)
# 누적합 예비 배열을 생성한다.
count_sum = [0] * (K)
for i in range(0, N):
count_sum[nums[i - 1]] += 1
# 누적합 배열을 만든다. (인덱스에 해당하는 값이 들어가야할 마지막 인덱스 번호를 가리킨다.)
for i in range(1, K):
counts[i] += counts[i-1]
# 배열의 값을 인덱스로 하는 누적합 배열을 찹조한다. -> 해당 값이 들어가야할 마지막 인덱스 번호
# 결과 배열의 해당 인덱스에 숫자를 집어넣는다.
# 다음 값을 위해 해당 값을 인덱스로 하는 누적합 배열의 값을 -1 한다.
# 내가 그린 기린 그림은 잘 그린 기린 그림이고...
result = [0] * N
for num in nums:
idx = count_sum [num]
result[idx - 1] = num
count_sum[num] -= 1
9. 복잡도 비교